
毎月3万円を積立て、金利3%の複利で運用したら、
10年後には一体いくらになっているだろう・・・
こんなことがパッと計算できたら、いいと思いませんか。
今回の記事を最後までお読みいただければ、それが簡単にできるようになります。
複利の「考え方」については、前回の記事でお話した通りです。複利で時間を味方につけた効果はバツグンってことでしたね。
まだお読みでない方はこちらからどうぞ。
今回は、定期的に積み立てをしながら、複利で運用する場合はどうなるのか、というお話です。
定期積立しながら複利運用した金額は、どうやって計算する?
実は、簡単な計算方法があります。
具体的にはこんな式です。
運用後の元利合計金額
=毎年の積立金額×係数
この係数は「年金終価係数」という名前がついていますが、小難しい名称自体はどうでもいいです。
積立金額に係数を掛ければ、積立てしながら複利運用した後の元利金合計が計算できる、ということを覚えておいてもらえればOKです。
係数はどうやって見たらいいのか
私の方で係数表を作成しました。
こちらをご覧ください。
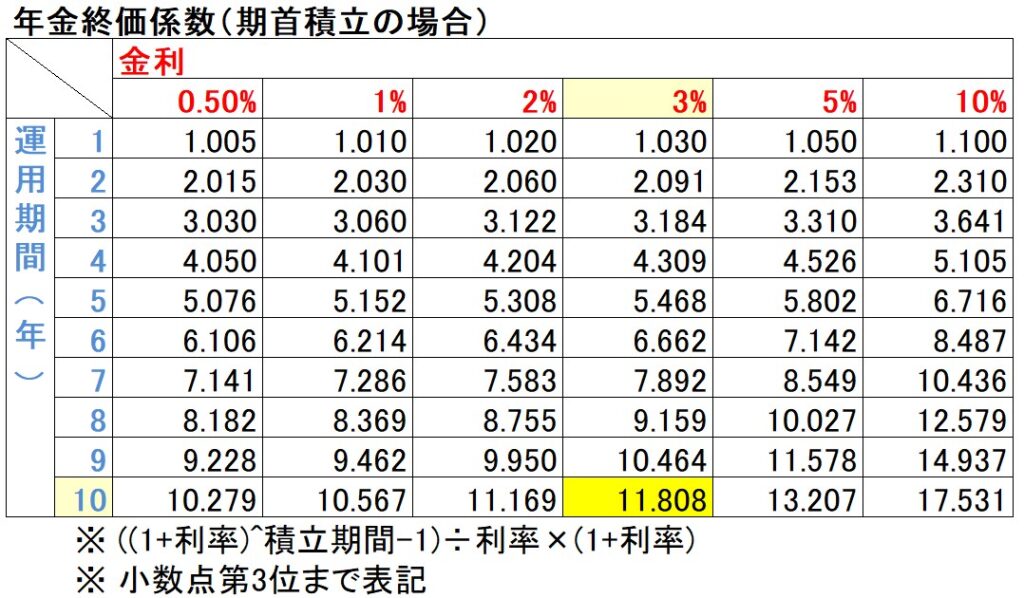
例えば、毎年年初に10万円ずつ積み立てていくとします。
運用期間(積立期間)10年間、3%の金利で運用するとなると、係数はこの表で10年と3%がぶつかったところ、すなわち、11.808が計算に用いる係数です。
すると10年後の元利金合計はこのように計算できます。
10万円(積立額)×11.808(係数)
=118万800円(税引前)
10年間で積立てた額は100万円ですが、積立した元本は複利で運用されるので、18万円ほどの利息が付くことがわかります。※税金等は考慮していません。
年金終価係数はどうやって出すの?
あなたはここで、こんなことを思ったかもしれません。

積立額に係数を1回掛ければ、積立後の元利金合計を算出できることわかった。
でも、その係数(年金終価係数)ってどうやって出てきたんだ・・・?
結論から言うと、係数はこれで算出できます。(期首積立の場合)

これは高校の時にやった等比数列の和の公式から導き出されます。
ここまでくると、頭痛がしているかもしれないので、係数を導き出すための詳細な計算までは省略します。^^;
毎月積み立てる場合は、どうやって計算する?

実際の積立は、毎月なんだけど・・・その場合はどうなるの?
という疑問が浮かんでいるかもしれません。
毎月3万円コツコツ積み立てて複利で運用したら、10年後には元利合計でいくらになってる?みたいなやつですね。
この場合、年1回の積立を前提とした「年金終価係数」はそのままは使えません。
どうするか。
月次積立しながら、複利運用する場合の元利合計は、以下のように計算します。

※年利を12で割って、月利を計算
※月数というのは、積立回数なので積立年数×12ヵ月で計算
具体例で見てみましょう

元本は360万円(3万円×120回)ですが、およそ40万円近い利息がついていることがわかります。
係数で一発! 月次版の「年金終価係数」もつくってみた
毎月積立用の係数表を作ってみました。
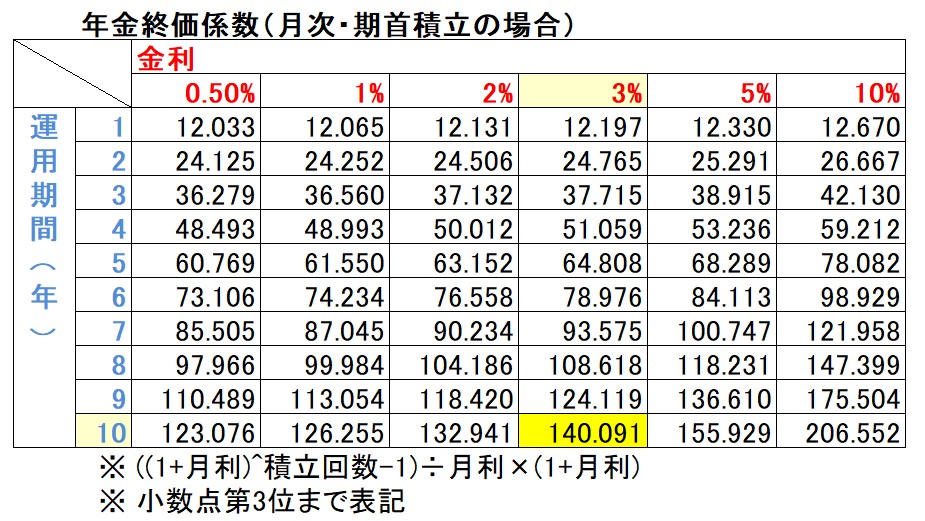
たとえば、年利3%・期間10年なら、係数は「140.091」です。(小数第3位まで)
この数字さえわかれば、さっきのように、
毎月の積立額×係数で将来の元利合計額
でパッと計算できるわけです。
掛け算1回で算出することができるので便利ですね。
まとめ|「毎月の積立 × 複利」のチカラ
今回ご紹介したように、「毎月の積立」を「複利」で運用するだけで、時間とともにお金は驚くほど大きく育っていきます。
- 3万円を10年間、月利0.25%で積み立てると約434万円に
- 複利効果によって、元本360万円に対して約74万円の利息がつく計算に
月々コツコツの積み重ねも、「時間を味方につける」ことでここまでの差が生まれます。
これは知っているかどうか、やっているかどうかだけの違いです。
おまけ|「お金の話」って、自分ごとにしにくい?
「投資とか運用って、なんだか遠い話」
「自分には関係ない気がする」
そんな声をよく耳にします。
でも実際には、**毎月の積立も、老後の備えも、家の管理や相続も、全部“お金の話”**です。
株式会社まっとうでは、不動産や相続に関わる「お金まわりのご相談」も承っています。
今すぐ何かを決める必要はありません。
「モヤモヤしてるけど、誰に聞いたらいいか分からない…」
そんなときは、一度お気軽にお声がけください。








